Where Would A Bevel Gear Be Used
Bevel Gears
Introduction
This article gives y'all a comprehensive look on bevel gears. This guide gives you the following data.
- What is a bevel gear?
- Efficiency of bevel gears and a comparing to other gear types
- Bevel gear types
- Geometry and terminologies
- Manufacturing processes
- Applications of Bevel Gears
- And much more than…

Chapter i: What is a Bevel Gear?
A bevel gear is a toothed rotating motorcar element used to transfer mechanical energy or shaft ability between shafts that are intersecting, either perpendicular or at an angle. This results in a change in the axis of rotation of the shaft ability. Bated from this office, bevel gears can also increase or decrease torque while producing the opposite effect on the athwart speed.
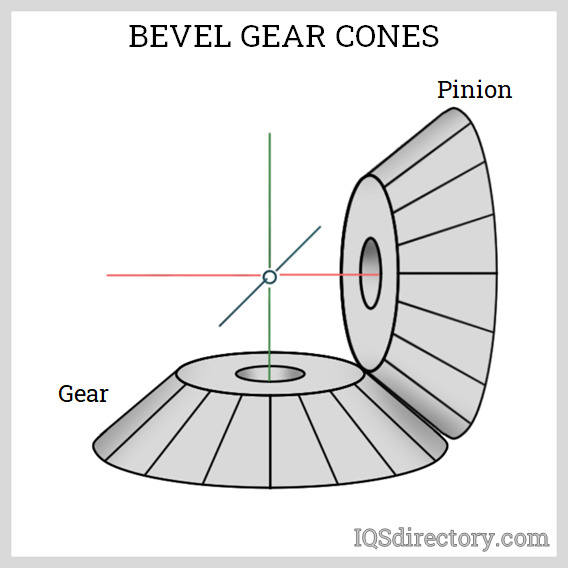
A bevel gear can be imagined as a truncated cone. At its lateral side, teeth are milled which interlock to other gears with its own ready of teeth. The gear transmitting the shaft power is chosen the driver gear, while the gear where power is being transmitted is chosen the driven gear. The number of teeth of the driver and driven gear are usually different to produce a mechanical advantage. The ratio between the number of teeth of the driven to the driver gear is known equally the gear ratio, while mechanical advantage is the ratio of the output torque to the input torque. This relationship is shown past the following equation:
\begin{equation} \ MA = \frac{T_b}{T_a} = \frac{r_b}{r_a} = \frac{N_b}{N_a} \end{equation}
MA is the mechanical advantage, τb and τa are the torques, rb and ra are the radii, and Nb and Na are the number of teeth of the driven and driver gears, respectively. From the equation, it tin exist seen that increasing the number of teeth of the driven gear produces a larger output torque.
On the other hand, producing a larger mechanical advantage decreases the driven gears output speed. This is expressed by the equation:
\brainstorm{equation} \ MA = \frac{W_a}{W_b} \cease{equation}
ωª and ωb are the driver and driven gears' angular speed, respectively. In general, a gear ratio of ten:1 is recommended for a bevel gear ready. For increasing the speed of the driven gear, a gear ratio of 1:5 is suggested.

Note that bevel gears are ordinarily a paired prepare and should not exist used interchangeably. Bevel gears are assembled in a specific style due to its inherent manual of both thrust and radial loads, in contrast with spur gears which by and large transmit radial loads simply. All bevel gears are assembled at its optimum position for best performance.
Chapter two: Efficiency of a Bevel Gear
Efficiency is divers as the ratio of the output power to the input ability. Note that this is different with mechanical advantage that is concerned with the amplification of forces or torques by sacrificing speed. When it comes to bevel gears, loss of ability during transmission is attributed to friction due to sliding between teeth surfaces and loads applied to the bearings or housing. Efficiency of dissimilar types of bevel gears compared with other types are summarized by the table below.
| Type of Gear | Approximate Range of Efficiency | Type of Load Imposed in Bearings |
|---|---|---|
| Straight Bevel Gear | 97 – 99.five% | Radial and thrust |
| Spiral Bevel Gear | 97 – 99.v% | Radial and thrust |
| Zerol Bevel Gear | 97 – 99.v% | Radial and thrust |
| Hypoid Bevel Gear | 90 – 98% | Radial and thrust |
| External Spur Gears | 97 – 99.5% | Radial |
| Internal Gears | 97 – 99.v% | Radial |
| Worm Gear | 50 – xc% | Radial and thrust |

GET YOUR Visitor LISTED Below
Leading Manufacturers and Suppliers
Chapter 3: Types of Bevel Gears
There are unlike types of bevel gears according to their tooth profile and orientation. The more than complicated types such as the spiral and hypoid bevel gears resulted from further evolution of manufacturing processes such as CNC machining.

-
Directly Bevel Gears
This is the simplest form of a bevel gear. The teeth are in a straight line which intersects at the axis of the gear when extended. The teeth are tapered in thickness making the outer or heel part of the molar larger than the inner role or toe. Straight bevel gears accept instantaneous lines of contact, permitting more tolerance in mounting. A downside in using this type is the vibration and noise. This limits straight bevel gears to low-speed and static loading applications. Mutual application of straight bevel gears are differential systems in automotive vehicles.
Directly bevel gears are the easiest to industry. The primeval manufacturing method for producing a directly bevel gear is past using a planer with an indexing head. More than efficient manufacturing methods have been made post-obit the introduction of Revacycle and Coniflex systems, employed by Gleason Works.

-
Spiral Bevel Gears
This is the most circuitous form of bevel gears. The teeth of spiral gears are curved and oblique, in dissimilarity to the teeth orientation of straight bevel gears. This results in more overlap between teeth which promotes gradual date and disengagement upon molar contact. This improved smoothness results in minimal vibration and noise produced during operation. Also, because of higher load sharing from more teeth in contact, screw bevel gears have better load capacities. This allows them to exist smaller in size compared to straight bevel gears with the aforementioned capacity.

A disadvantage of spiral bevel gears is the larger thrust load exerted which requires more expensive bearings. A rolling element thrust bearing is usually required for spiral bevel gear assemblies. Too, spiral bevel gears are made in matched sets. Different gear sets with the aforementioned design are not interchangeable unless purposely built to. Spiral bevel gear sets are fabricated either correct-mitt or left-hand.
Spiral bevel gear teeth are typically shaped past gear generating types of machines, which will be discussed in depth later. This process creates high accurateness and terminate. Besides, lapping is done to finish the teeth and further obtain the desired tooth bearing.
-
Zerol Bevel Gears
This type is a modification of a directly bevel gear trademarked past Gleason Works. Zerol bevel gears have teeth curved in the lengthwise direction. These gears are also somewhat similar to screw bevel gears in terms of its profile. Their difference is the screw angle; Zerol types accept 0° screw angles while screw types have 35°.

Similar the straight bevel gears, Zerol types practice non produce excessive thrust loads. Thus, plain contact bearings can be used. Zerol types can be substituted with straight bevel gears without irresolute the housing or bearings. Moreover, due to its curvature, Zerol bevel gear teeth have a slight overlapping action similar to spiral gears. This makes the gears run smoother than direct bevel gears.
Zerol bevel gear teeth are generated by a rotary mill cutter. The curvature of this cutter makes the lengthwise curvature of the tooth. Zerol bevel gears are cutting at a loftier precision, often finished by lapping or grinding.
-
Hypoid Bevel Gears
This is a special type of bevel gears where the axes of the shafts are non intersecting nor parallel. The distance betwixt the two gear axes is called the offset. The teeth of hypoid bevel gears are helical, similar to spiral bevel gears. A hypoid bevel gear designed with no offset is simply a spiral bevel gear. Manufacture and shaping of hypoid types are like to spiral bevel gears.
Considering of the get-go, the spiral bending of the smaller gear (pinion) of a hypoid bevel gear set tin be made larger than the spiral diameter of the larger gear. The ratio of the number of teeth of the gears are not directly proportional to the ratio of their pitch diameter or the theoretical operating diameter of the gear. This makes it possible to match larger pinions to a particular size of a driven gear, making the pinion stronger and accept a college contact ratio to the larger gear. In plough, information technology allows hypoid gears to transmit more torque and operate at higher gear ratios. Also, with enough commencement, bearings on both sides of the gears can exist placed since their shafts are not intersecting. The merchandise-off, however, is the decrease in efficiency as the offset is beingness increased.

Hypoid gears operate smoother with minimal vibration than spiral gears. The downside of using spiral gears, aside from the efficiency event mentioned before, is the high sliding that takes place across the face up of the teeth. This means special lubricating oils must be used.
-
Miter Bevel Gears
This is a type of bevel gear with a gear ratio of ane:ane, meaning the driver and driven gears take the same number of teeth. The purpose of this type is express to changing the axis or rotation. It does not produce any mechanical advantage. Usually, miter gears have axes that intersect perpendicularly. In some assemblies, the shafts are aligned to intersect at any angle. These are known every bit angular miter bevel gears. Shaft angles of angular miter bevel gears tin range from 45° to 120°. Miter bevel gear teeth cuts can be straight, spiral, or Zerol.

Affiliate four: Geometry and Terminologies
To better understand gears and gear systems, i must first look at its terminologies. Below are some of the terms used to describe gears and their tooth profile. These are applicative for all types of gears, non only bevel gears.

Pinion
The smaller bevel gear in a bevel gear set.
Gear
The larger bevel gear in a bevel gear set.
Pitch
Also known as round pitch, is the distance from 1 point on a tooth to the corresponding signal of the side by side molar on the same gear.
Pitch bore
The diameter of the pitch circumvolve. This is a predefined blueprint dimension where other gear characteristics such equally molar thickness, pressure angles, and helix angles are adamant.
Diametral pitch
The ratio of the number of teeth and the pitch diameter.
Pitch angle
The angle betwixt the confront of the pitch surface and the shaft axis.
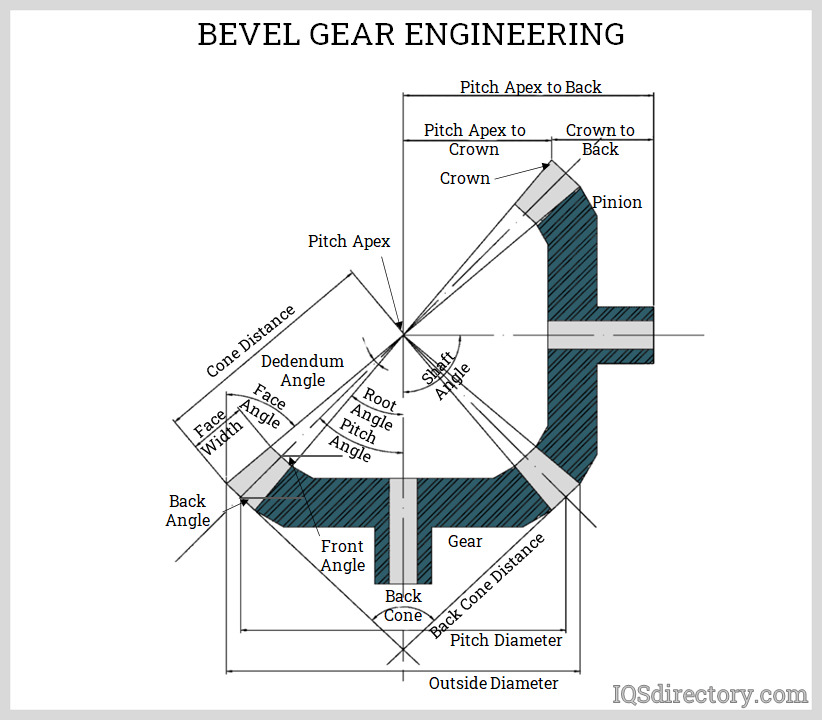
Pitch surface
The imaginary truncated cone wherein the base of operations diameter is the pitch circle.
Pressure angle
A predefined value which is described by the angle betwixt the line of force of the meshing teeth and the line tangent to the pitch circle at the contact indicate. Gears must have the aforementioned pressure angle in order to mesh. The recommended pressure angles for straight bevel gears is 20°.
Shaft bending
A predetermined value that defines the angle between the driven and driver shafts.
Annex
The upper outline of the gear teeth.
Dedendum
The bottom outline of the gear teeth.
Total depth
The radial altitude between the addendum and dedendum circles of a gear. Note that the teeth of a bevel gear are slightly tapered, thus the total depth is not constant along the tooth. Considering of this, the addendum and dedendum angles are used to describe the teeth instead of the addendum and dedendum circles.
Addendum angle
The angle betwixt the face of the upper surface of the teeth or top country and the pitch surface.
Dedendum angle
The angle betwixt the lesser surface of the teeth or bottom land and the pitch surface.
Depth of taper
The change in tooth depth along the face measured perpendicular to the pitch surface.
Space width taper
The alter of the space width along the face measured on the pitch surface.
Thickness taper
The change of tooth thickness measured on the pitch surface.
Working depth
The total depth of the teeth plus the value of the clearance.
Clearance
The difference between the annex of a gear to the dedendum of the mating gear.
Backfire
The amount of space that exceeds the thickness of a mating gear tooth. For bevel gears, there are different types of backfire depending on orientation of the movement. These are:
-
Circular
The arc along the pitch circumvolve
-
Normal
The space betwixt the surface of the mating teeth
-
Athwart
The described as the athwart movement
-
Radial
The linear move perpendicular to the axis
-
Axial
The linear movement parallel to the axis
Backlash is necessary to prevent the gears from jamming due to contact. This space allows for lubricants to enter and protect the surfaces of the mating teeth. Also, the backlash allows thermal expansion during functioning.
The relationship betwixt these terms are shown by the table of equations beneath.
| To Find | Having | Formula |
|---|---|---|
| Pitch bore of pinion | Number of pinion teeth and diametral pitch | d = Np / Pd |
| Pitch diameter of gear | Number of gear teeth and diametral pitch | D = Ng / Pd |
| Pitch angle of pinion | Number of pinion teeth and number of gear teeth | γ = tan ^-ane (Np / Ng) |
| Pitch angle of gear | Pitch angle of pinion | Γ= 90°-γ |
| Outer cone distance of pinion and gear | Gear pitch diameter and pitch angle of gear | Ao = D / (2sinΓ) |
| Round pitch of pinion and gear | Diametral pitch | p = 3.1416 / Pd |
| Dedendum angle of pinion | Dedendum of pinion and outer cone distance | δp = tan -1 (bop / Ao) |
| Dedendum angle of gear | Dedendum of gear and outer cone distance | δg = tan -1 (bog / Ao) |
| Confront angle of pinion blank | Pinion pitch bending and dedendum bending of gear | γo = γ + δg |
| Face angle of gear blank | Gear pitch angle and dedendum bending of pinion | Γo = Γ + δp |
| Root bending of pinion | Pitch angle of pinion and dedendum angle of pinion | γr = γ - δp |
| Root angle of gear | Pitch angle of gear and dedendum angle of gear | Γr = Γ - δg |
| Outside bore of pinion | Pinion pitch diameter of gear, pinion addendum, and pitch angle of pinion | do = d +2aop cosγ |
| Exterior bore of gear | Pitch diameter of gear, gear annex, and pitch bending of gear | Do = D + 2aog cosΓ |
| Pitch apex to crown of pinion | Pitch diameter of gear, annex, and pitch bending of pinion | xo = (D/2) - aop sinγ |
| Pitch apex to crown of gear | Pitch diameter of pinion, addendum, and pitch angle of gear | Xo = (d/2) - aog sinΓ |
| Circular tooth thickness of pinion | Circular pitch and gear circular tooth thickness | t = p - T |
| Chordal thickness of pinion | Circular tooth thickness, pitch diameter of pinion and backlash | tc = t - (t3/6d2) - (B/ii) |
| Chordal thickness of gear | Round tooth thickness, pitch diameter of gear and backlash | Tc = T - (T3/6D2) - (B/2) |
| Chordal addendum of pinion | Addendum angle, circular tooth thickness, pitch diameter, and pitch angle of pinion | acp=aop + (t2 cosγ / 4d) |
| Chordal annex of gear | Annex bending, circular molar thickness, pitch bore, and pitch angle of gear | acg=aog + (T2 cosΓ / 4D) |
| Tooth angle of pinion | Outer cone distance, molar thickness, dedendum of pinion, and pressure angle | (3.438/Ao)(t/2)+bop tanφ min |
| Tooth angle of gear | Outer cone distance, tooth thickness, dedendum of gear, and pressure angle | (3.438/Ao)(T/2)+bog tanφ min |
| To Find | Having | Formula |
|---|---|---|
| Pitch diameter of pinion | Number of pinion teeth and diametral pitch | d = Np / Pd |
| Pitch diameter of gear | Number of gear teeth and diametral pitch | D = Ng / Pd |
| Pitch angle of pinion | Number of pinion teeth and number of gear teeth | γ = tan -1 (Np / Ng) |
| Pitch angle of gear | Pitch angle of pinion | Γ= 90°-γ |
| Outer cone distance of pinion and gear | Pitch bore of gear and pitch angle of gear | Ao = D / (2sinΓ) |
| Circular pitch of pinion and gear | Diametral pitch | p = 3.1416 / Pd |
| Dedendum angle of pinion | Dedendum of pinion and outer cone distance | δp = tan -1 (bop / Ao) |
| Dedendum bending of gear | Dedendum of gear and outer cone distance | δg = tan -i (bog / Ao) |
| Face angle of pinion bare | Pitch angle of pinion dedendum angle of gear | γo = γ + δg |
| Face angle of gear blank | Pitch angle of gear and dedendum angle of pinion | Γo = Γ + δp |
| Root angle of pinion | Pitch angle of pinion and dedendum bending pinion | γr = γ - δp |
| Root bending of gear | Pitch angle of gear and dedendum angle of gear | Γr = Γ - δg |
| Outside diameter of pinion | Pitch bore, addendum, and pitch angle of pinion | practice = d +2aop cosγ |
| Outside diameter of gear | Pitch diameter, addendum, and pitch bending of gear | Practice = D + 2aog cosΓ |
| Pitch apex to crown of pinion | Pitch diameter of gear, pitch angle, and addendum of pinion | xo = (D/2) - aop sinγ |
| Pitch apex to crown of gear | Pitch bore of gear, pitch angle, and addendum of gear | Xo = (d/2) - aog sinΓ |
| Round tooth thickness of pinion | Circular pitch of pinion and circular pitch of gear | t = p - T |
Chapter 5: Manufacturing Processes
There are four main methods of manufacturing gears. These are metal cut, casting, forming, and powder metallurgy. Metallic cutting is the almost widely used procedure because of its dimensional accuracy. The other 2, casting and forming, are used in special circumstances such equally producing a large gear through casting which reduces machining expenses by casting closer to the final shape. Another form of casting, known as injection molding, is used to manufacture plastic gears. Forming, on the other paw, can be cold drawing or forging. Common cold drawing involves a stock to be pulled or extruded into a series of dies to course the shape of the gear. Forging presses the stock against dies with the desired tooth configuration. Because of work hardening through continuous deformation, the resulting gear is harder with a more contoured grain flow.

Gear cutting tin can be divided into four more classifications summarized beneath.
- Rotating threaded tool: hobbing, generating
- Rotating and reciprocating tool: shaping, shaving, generating
- Rotating disc wheel: milling, form grinding, thread grinding
- Linear motion tool: broaching, punching

Because of its conical shape resulting in a depth and width taper, non all techniques can exist practical for bevel gears. For bevel gear cutting, metal cutting techniques tin be categorized into two: face hobbing and face up milling.
- Face up Hobbing: Confront hobbing is a continuous indexing gear generation process. This involves groups of cutting blades that cut all teeth gradually until the desired depth is achieved. As one bract group cuts 1 tooth, the next blade group enters the adjacent molar space. The cutting tool and the workpiece rotate simultaneously.

- Face Milling: Confront milling is a single indexing method where the cutting cycle or tool is fed to cut one molar space and is then indexed to the next tooth location. The cutting tool and the workpiece are synched together to perform the cut. Each molar is milled until all teeth are cutting to the required depth. Face milling tin be washed by two-tool planer, double rotary blade, single row manufactory cutter, or five-axis CNC milling machines.

- Powder Metallurgy: Pulverization metallurgy is a process in which metal powders are formed into products or materials. In its most basic form, this is achieved by pulverising the desired textile into a pulverization, compacting the powder into a die, and then sintering. This manufacturing process is valued due to the fact that metallic removal processes are frequently not needed for secondary finishing, which results in less waste and therefore lower costs. Gears that are formed by this process are lighter and brand less racket, due to their naturally porous nature.
Affiliate 6: Bevel Gear Applications
The use of bevel gears is one of the simplest and well-nigh efficient methods of changing a drivetrains' axis of rotation. The blazon of bevel gear and manufacturing and finishing processes used depends on the type of application. Below are some of the applications of bevel gear systems.
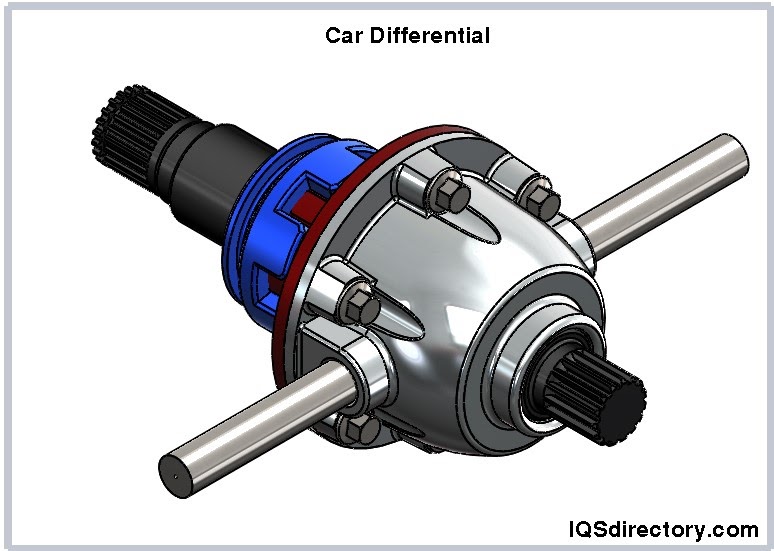
Automotive
The most popular application of bevel gears is the differential of an automotive vehicle. The differential is the part of the front or rear axle assembly that allows the wheels to rotate at unlike speeds. This allows the vehicle to turn corners while maintaining handling and traction. The driveshaft is connected to the hypoid gear assembly consisting of a pinion and a ring gear. The ring gear is mounted to the carrier with other bevel gears in a planetary gear train.
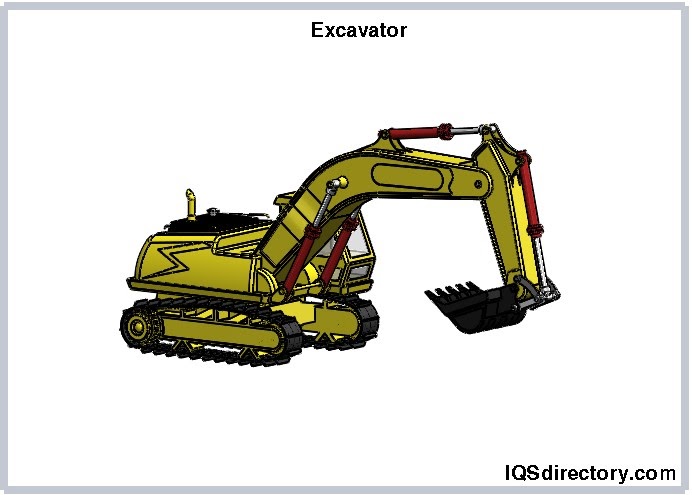
Heavy Equipment
Bevel gears are used by heavy equipment either for propulsion, the same as an automotive differential system, or for auxiliary units.
Aviation
Bevel gears are used in the aviation industry for ability transmission systems of helicopters and shipping accessory gearbox drivers.
Industrial Plant Equipment
An example of an industrial plant equipment that uses bevel gears are cooling tower fans. The motor is unremarkably mounted at the deck of the cooling tower with the shaft axis oriented horizontally. A gearbox assembly reduces the speed and increases the torque while also reorienting the centrality of rotation vertically.

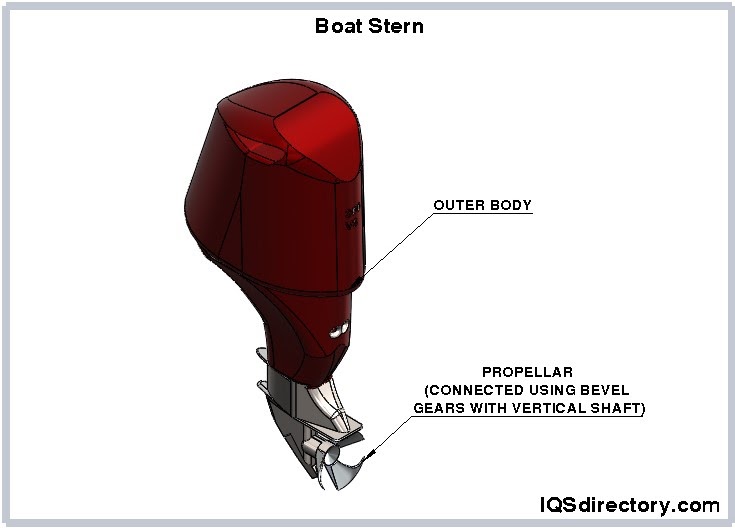
Marine
Bevel gears are unremarkably used in marine transmission every bit role of the stern drive. There are 2 bevel gear sets used betwixt the engine and the propeller.
Conclusion:
- Bevel gears are rotating auto elements used to transmit mechanical power between 2 intersecting shafts, either perpendicular or at an bending. Aside from changing the axis of rotation, bevel gears tin can likewise produce a mechanical advantage by increasing the output torque.
- Producing a mechanical advantage, withal, decreases the angular speed of the driven shaft. Thus, bevel gears can also be used equally speed reduction mechanisms.
- Efficiency is the ratio between output power and input power. Ability loss from bevel gears are more often than not due to friction from sliding contact. This is then dissipated as heat which is usually removed by lubricating oils.
- Bevel gears are classified according to the tooth contour and orientation. The types of bevel gears are directly, screw, Zeroil, and hypoid.
- Efficiencies of bevel gears range from 97-99.5%, except for the hypoid bevel gears with an efficiency of 90-98%. A larger offset of a hypoid gear causes further decrease in efficiency.
- There are many terms used to describe gears. The nearly important for bevel gears are the pitch diameter, pressure angle, shaft angle and number of teeth. These are the key values which will define the geometry of the gear.
- At that place are 3 primary methods of manufacturing gears: cutting, casting, and forming. Among the 3, cutting is the almost widely used.
- Gear cutting is further cleaved down into several methods. I is by using a rotating threaded tool such equally a hob. Next is past using a rotating or reciprocating cut tool that mates together with the gear blank. Third is cut using a rotating disc bike every bit seen from milling processes. And lastly, gear cut using a linear shaper or broaching tool.
- The about popular application of bevel gears is the automotive differential. This is seen not only on automotive vehicles, but as well in light and heavy equipment. Other main uses are in the aviation and marine industry.
Get YOUR COMPANY LISTED Below
Leading Manufacturers and Suppliers
Where Would A Bevel Gear Be Used,
Source: https://www.iqsdirectory.com/articles/gear/bevel-gear.html
Posted by: handyowly1985.blogspot.com


0 Response to "Where Would A Bevel Gear Be Used"
Post a Comment